

Introducción
Todo sistema mecánico existente es capaz de vibrar, en este
laboratorio hacemos ensayos con un sistema torsional que posee masa y
elasticidad específicamente, sabemos que un cuerpo se mantendrá en reposo hasta
que se le aplique una fuerza externa sobre él.
Un
sistema torsional sale del reposo cuando esta fuerza externa previamente
mencionada es un desplazamiento y/o una velocidad angular. En caso de que el
sistema no posea amortiguamiento el mismo oscilará con respecto a la posición
de equilibrio y tendrá un periodo natural definido. La ecuación que describe
este movimiento es una ecuación diferencial homogénea de segundo grado con
coeficientes constantes.
Hay
ciertos parámetros que definen este sistema como lo son la frecuencia natural dada
en Hz y definida por la ecuación
Es
decir, que la frecuencia natural del sistema es inversamente proporcional al
periodo natural del mismo. También se puede definir la frecuencia natural
circular del sistema dada en radianes por segundo y se puede determinar por
medio de estas dos ecuaciones:
Por último, definimos la ecuación diferencial del movimiento como:
Equipo y materiales a utilizar
- Instrumento de medida (Pie de rey)
- Llave para tornillos
- Llaves para aflojar la barra
- Discos de masa (inercias)
- Pernos
- Barra (resorte de torsión)
- Barras de masa (inercias)
- Marco para soporte
- Se utilizó una llave L para ayudar a aflojar la barra, debido que la del laboratorio presentaba defectos en su funcionamiento.
Procedimiento

- Se tomaron las medidas de los diámetros correspondientes de la barra de torsión, barras de masa, y las masas de inercia correspondientes.
- Se desplazó el apoyo, opuesto a los discos, para lograr la máxima longitud posible de la barra de torsión.
- Se procedió a remover los dos discos satélites, verificando que las barras de soporte estuvieran en posición horizontal.
- Se fijó el apoyo opuesto a la inercia.
- Se llevaron las barras a un ángulo inicial y se anotó el tiempo para tres ciclos de oscilación.
- Se realizó el procedimiento anterior, pero ahora colocando los discos satélites en el sistema.
- Se determinó analíticamente la frecuencia circular y el periodo natural del sistema masa resorte.
- Desplazamos el apoyo, opuesto a los discos para fijar la longitud de la barra a la mitad de la longitud anterior.
Resultados
 |
| Tabla 2.1. Respuesta de oscilación de un péndulo torsional. |


Preguntas
Compare las frecuencias
naturales de oscilación, para los sistemas disco-resorte torsional obtenidas de
forma experimental y analítica. Calcule y registre los porcentajes de error.
Explique las posibles fuentes de error en la realización del laboratorio.
 |
Tabla 2.2. Comparación de porcentajes de error.
Tal como se aprecia en el cálculo de error al analizar los
sistemas con satélites vs sin satélites, sin duda el error para un sistema con
satélites parece aumentar de manera considerable, esto puede ser por algunas
consideraciones tales como, el hecho de que mientras mayor cantidad de
elementos se agreguen en la medición para un sistema dado, aumenta las
probabilidades de que este error se eleve.
Entre las posibles causas de error, son que al realizar la
medición contamos con sistema totalmente real, que implican una serie de
agentes que pueden afectar, tales como los errores de medición (por
instrumentos ó por simple error humano), posibles imperfecciones de los
materiales expuestos al experimento realizado.
¿Qué aproximaciones son
necesarias para la simplificación del modelo matemático estudiado en el
laboratorio?
- Para la simplificación de dicho modelo se asumió que el
sistema evaluado era de un grado de libertad (1 GDL) y que la masa era
totalmente uniforme.
A partir de los resultados
explique qué efecto tiene sobre el periodo y la frecuencia natural al
incrementar el momento de inercia de un sistema.
- Al aumentar dicho momento de inercia, aumentara el periodo mientras
que la frecuencia natural disminuye.
A partir de los resultados
explique qué efecto tiene sobre el periodo y la frecuencia natural al disminuir
el momento masa de inercia de un sistema.
- Disminuye el periodo y aumentara la frecuencia de
oscilación.
A partir de los resultados
explique qué efecto tiene sobre el periodo y la frecuencia natural al incrementar
la elasticidad de un sistema.
- Al incrementar la elasticidad del sistema estaremos
aumentando automáticamente el periodo, mientras que su frecuencia disminuye.
A partir de los resultados
explique qué efecto tiene sobre el periodo y la frecuencia natural al disminuir
la elasticidad de un sistema.
- Sera lo contrario a la pregunta anterior, es decir que el
periodo disminuirá mientras que la frecuencia aumentará.
¿Cuál es su conclusión general
sobre las características dinámicas de un sistema torsional?
- Para un sistema sometido a torsión claramente es importante
un análisis dinámico para el diseño de un elemento, ya que este nos puede
brindar características relevantes en cuanto a la vibración del sistema. El
cual puede ser aprovechado para prevenir o evitar que un sistema falle por
dicho fenómeno, ya que un una gran cantidad de sistemas mecánicos estas vibraciones
pueden jugar un papel clave y a su vez pueden ser perjudiciales para el
satisfactorio funcionamiento de un sistema dado.
Conclusión
El desarrollo de esta experiencia nos ayudó a desarrollar y analizar el modelo físico y matemático de un sistema disco-resorte torsional. Fuimos capaces de determinar la características principales de los componentes de un sistema dinámico y, también, determinar el momento de inercia de los discos y barras respecto al eje de rotación. Por último, pudimos medir el periodo natural de la vibracoón libre que resulta de un sistema dinámico torsional, a la vez, compararmos los resultados, tales como el efecto en la variación de los discos y/o elasticidad del sistema.
Publicado por:
Grupo 1EM131
Arrocha, Stephani 2-737-2147
Ayarza, Ian 4-771-2035
Cárdenas, Jean Pierre 20-70-2008
Mendoza, Jellini 8-915-1006
Vásquez, Jorge 8-914-195
|









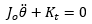
















Comentarios
Publicar un comentario